CSE 470 Assignment 3 Part 2 - Gourad/Phong Shading
This is a continuation from part 1 of this blog, which you can read here
Part 1 of this blog covered the math behind creating a surface of revolution, and this part 2 will cover the math behind the Phong illumination model and different methods of implementation.
The Phong illumination model is an approximation of physical lighting calculations based around the idea that you have three main components of the way a surface responds to being lit:
- Ambient
- Diffuse
- Specular
Ambient is the way the surface will look if no light source is being shined directly on it. This is used to approximate the effects of global illumination in a time efficient manner. For example, if you're in a room with all blue walls and you shine a white light on a white object, it will be mostly white where it is lit, but on the shadow sides it will be blue because of the reflected light from the room. This is the ambient term. You can see an example of how a scene with no ambient light vs with some ambient light looks here:

Diffuse describes the way a matte (not glossy) surface will react to being lit. It is a smooth gradient as the surface turns towards/away from the light source. This effect happens because of small variations in the surface of the object which reflect the light that hits it in various directions, some which will reach the viewer and some which will not. Actually, there is a bit more going on here, but that's for another blog post where we talk about 'physically based' lighting.
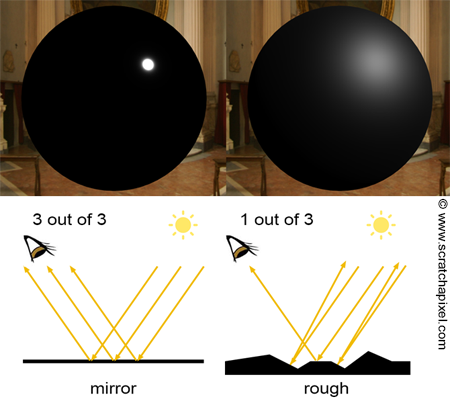
Specular describes the way a glossy (shiny) surface will react to being lit. It results in a harsh highlight which is usually quite sharp based on the angle between the surface, the light, and the viewer. This effect happens when there are few surface imperfections and so light is allowed to reflect perfectly or close to perfectly, and therefore will only reach the viewer if the angle matches up correctly. In non-metal objects, this specular highlight will always be white, no matter the color of the object. In metallic objects, the specular highlight will have coloration.
Here we see an example of what purely specular and diffuse lighting looks like and why they occur:
Finally you can see an example of how these properties sum together here:

We can combine different weights of these components together to create an approximation of varying accuracy of many different materials. In the Phong model, these weights are often labeled `kappa_a`, `kappa_d`, and `kappa_s` which correspond to the ambient, diffuse, and specular weights respectively. In addition, there is one more constant, called the shininess or attenuation constant (which I will label `alpha`), which controls how tight the specular reflection is. Higher values correspond to shinier surfaces and therefore tighter (smaller) specular highlights.
In addition to these four constants, we have a few others we use as well. First are the colors for each of the ambient, diffuse, and specular for the material, which we'll call `C_(ma)`, `C_(md)`, and `C_(ms)`. Then we have the light color, which we'll call `C_l`.
The way that the lighting calculations work is by creating a mathematical equation which takes as input the location of a point on a surface and gives as output the final, lit color of that surface. In addition to the location of the point on the surface, we'll need a few other pieces of information, namely the surface normal of the object at that point on the surface, the location of the light which is shining on the surface and the location of the camera or viewer which is looking at the object. These will help us derive the following vectors which will be used in the calculations.
- The surface normal vector at the point in question, which we'll call `hat N`
- The vector from the point to the light, `hat L`
- The vector from the point to the viewer, `hat V`
- The perfect reflection vector of the light off the surface, `hat R`
The hats here signify that the vectors need to be normalized (have a length of 1).
You can see an illustration of these here (ignore H, it's not used yet):

Finally we can put all this together to find the total illumination/color for any point `p` on an surface, `I_p`, given a set of lights that are shining on that object:
`I_p = kappa_a C_(ma) + sum_(i in lights) (kappa_d C_(md) C_(l,i)(hat L_i cdot hat N) + kappa_s C_(ms) C_(l,i)(hat R_i cdot hat V)^alpha)`
While this may look a bit complicated at first, it's not too bad once we dissect it a little bit. Essentially what's happening is that we are adding together each of the ambient, diffuse, and specular terms. The ambient term is the simplest, just a multiplication of the ambient coefficient times the material's ambient color:
`kappa_a C_(ma)`
Next we have a sum for each of the lights, which means we'll repeat the following steps for each light we want to take into account and then sum each result. First we calculate the diffuse term:
`kappa_d C_(md) C_(l,i)(hat L_i cdot hat N)`
This is just multiplying together the diffuse coefficient with the diffuse color of the material, the color of the light in question, and the dot product between the vector to the light and the normal vector. The dot product between two normalized vectors will give us the cosine of the angle between the two vectors, which ranges from -1 to 1, 1 meaning `hat L_i` and `hat N` are pointing in the same direction and -1 meaning they are opposite, 0 meaning they are perpendicular. Since we only care about until we get to perpendicular (light doesn't curve around objects, at least at this scale), we can clamp this value from 0 to 1. This means the diffuse term is independent of the viewer position and varies based on how directly the surface is pointed at the light source. Next we have the specular term:
`kappa_s C_(ms) C_(l,i)(hat R_i cdot hat V)^alpha`
This is quite similar to the diffuse term, just using the specular constants and colors, except that now we take the dot product of the reflection vector of the light, `hat R_i`, and the vector to the viewer, `hat V`. That means the specular term is varied based on the alignment of the viewer and the reflection vector; when they are close, we will see a specular highlight, and when they are far apart we will not. Notice that this is different from the diffuse term, which means that the specular highlight will not always (and in fact most of the time will not) be in the same place as the lightest part of the diffuse illumination. In addition, we raise this dot product to the power of `alpha`, our shininess constant. Since our range is between 0 and 1, raising it to a higher power will mean the falloff will be more severe and cause a sharper specular highlight.
So now that we have a way to calculate the color of any point on the surface, we can simply apply this formula in a fragment shader, passing through the needed information about the materials, lights, normals, etc. Alright, I think that's going to wrap up this blog post. In a subsequent one I'll go through the actual implementation of this theory in a fragment shader code, and then after that we'll dive in to 'Physically Based' rendering! I hope you enjoyed these couple of blog posts and have learned more about how surfaces of revolution and the Phong illumination model work.
Latest Posts
- A Whirlwind Tour of Games Color ManagementA coworker recently asked me this question during a discussion about color management and encoding. I wrote the original version of this…read more →
- ultraviolet 0.6 ReleasedIntroduction For those unfamiliar, ultraviolet is a crate to do computer-graphics and games-related linear algebra, but fast, both in terms…read more →